ESTADISTICA

Concepto

En palabras simples, la estadística es una ciencia que permite recolectar, ordenar y analizar datos (información) con el objetivo de tomar decisiones.

Población

Es el conjunto total de individuos, objetos o eventos que tienen las mismas características y sobre el que estamos interesados en obtener conclusiones. Es decir, es el conjunto total de elementos a estudiar.

Muestra

Es una parte de la población, la cual se selecciona con el propósito de obtener información. 

Variables

Son los caracteres o cualidades de la población que es objeto de estudio o análisis. pueden ser:

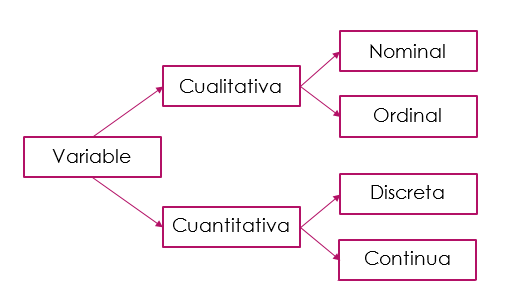
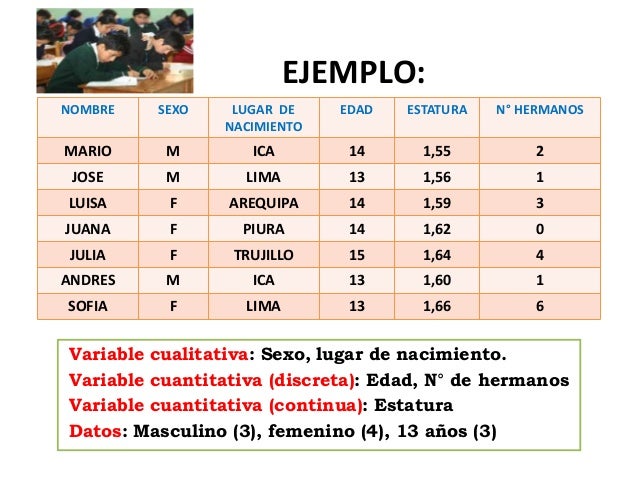
Las cualitativas no se pueden medir y se expresan con palabras. Tienen distintas modalidades, que son las diferentes situaciones que se pueden presentar. Por ejemplo: sexo: femenino-masculino,color de ojos,color de cabello.

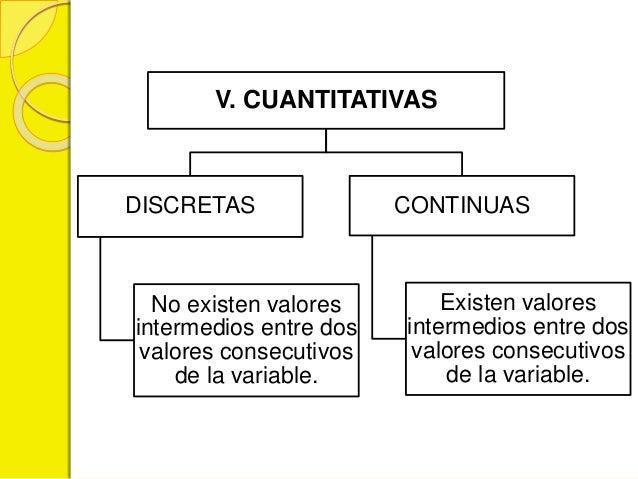
Las cuantitativas se pueden medir y se expresan por medio de un numero. 

Distribución de frecuencias

La distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.

Tipos de frecuencias

Frecuencia absoluta

La frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico.

Se representa por f_i.

La suma de las frecuencias absolutas es igual al número total de datos, que se representa por N.

Para indicar resumidamente estas sumas se utiliza la letra griega Σ (sigma mayúscula) que se lee suma o sumatoria.

Frecuencia relativa

La frecuencia relativa es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos.

Se puede expresar en tantos por ciento y se representa por n_i.

La suma de las frecuencias relativas es igual a 1.

Frecuencia acumulada

La frecuencia acumulada es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado.

Se representa por F_i.

Frecuencia relativa acumulada

La frecuencia relativa acumulada es el cociente entre la frecuencia acumulada de un determinado valor y el número total de datos. Se puede expresar en tantos por ciento.

xi	Recuento	fi	Fi	ni	Ni
27	I	1	1	0.032	0.032
28	II	2	3	0.065	0.097
29		6	9	0.194	0.290
30		7	16	0.226	0.516
31		8	24	0.258	0.774
32	III	3	27	0.097	0.871
33	III	3	30	0.097	0.968
34	I	1	31	0.032	1
		31		1

Elaboración de un histograma

Ejemplo:

Tenemos la siguiente distribución de edades de una población:

Estadística descriptiva e inferencial

ejemplos

Un fabricante de tornillos desea hacer un control de calidad. Para ello recoge uno de cada 100 tornillos fabricados y lo analiza. El conjunto de tornillos analizados, ¿es población o muestra?

el conjunto de tornillos analizados se lo llama muestra porque solo es una parte del total de tornillos fabricados.

Representaciones gráficas

Tablas: es una forma sencilla y clara de agrupar la información. Pueden ser sencillas o complejas según la cantidad de datos. Es importante el manejo lógico de la disposición.






                     
Gráficos: permiten visualizar la información y sus relaciones. Es una forma ilustrativa y clara de los datos. Es una forma creativa y artística de presentación.












En el siguiente vídeo les explicara de un manera muy dinámica los tipos de gráficas que hay en estadística.

juegos aleatorios : azar. 

PROBABILIDAD

Probabilidad

• La probabilidad mide la mayor o menor posibilidad de que se dé un determinado resultado (suceso o evento) cuando se realiza un experimento aleatorio.
• Para calcular la probabilidad de un evento se toma en cuenta todos los casos posibles de ocurrencia del mismo; es decir, de cuántas formas puede ocurrir determinada situación.
• Los casos favorables de ocurrencia de un evento serán los que cumplan con la condición que estamos buscando.

• La probabilidad toma valores entre 0 y 1 (o expresados en tanto por ciento, entre 0% y 100%):

1. El valor cero corresponde al suceso imposible; ejemplo: lanzamos un dado al aire y la probabilidad de que salga el número 7 es cero.
2. El valor uno corresponde al suceso seguro, ejemplo: lanzamos un dado al aire y la probabilidad de que salga cualquier número del 1 al 6 es igual a uno (100%).
3. El resto de sucesos tendrá probabilidades entre cero y uno: que será tanto mayor cuanto más probable sea que dicho suceso tenga lugar.

• Probabilidad (A) = (Número de casos favorables)/(Número de casos posibles)
• Ejemplos :

 En una clase de COU el 45% de los estudiantes suspende Matemáticas, el 60% suspende física y el 30% suspende ambas. Se selecciona al azar un alumno:

a) Si suspendió Física ¿Cuál es la probabilidad de que suspendiera Matemáticas?

b) Si suspendió Matemáticas  “                                        “           Física?

Solución

Sea  A = “suspende Matemáticas” y  B = “ suspende Física”

p(A) = 0,45; p(B) = 0,60 ; p(A Ç B) = 0,30

a) p(A/B) = 0,30/0,60 =1/2; p(B/A) = 0,30/0,45 = 2/3

FUNCIONES

FUNCIÓN LINEAL

• Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
• Puede reducirse a la forma:

F(X)= a . x + b

• El coeficiente A es la PENDIENTE y representa cuanto varía f(x) por cada unidad que aumenta X.
• El coeficiente B es la ORDENADA AL ORIGEN, es decir, el punto en el que la gráfica de la función corta al eje Y.
• La gráfica de una función lineal esta formada por puntos alineados, si está definida en su dominio natural, el conjunto R (real), la gráfica es una recta.

                       Ejemplo de representación gráfica:

Los valores de x son asignados arbitrariamente (aconsejable usar valores pequeños para facilitar las operaciones) luego en la ecuación remplazamos la x por cada valor de la tabla. 

                      y = 2x

       Para x = - 2, y = 2(-2) = -4  quedando la pareja (-2 , -4)

       Para x =  1,  y = 2(1)  =  2   quedando la pareja (1 , 2)

• El valor de la pendiente determina que una función sea creciente (a>0), constante (a=0), decreciente (a<0).

Función creciente

A medida que aumenta el valor de x, aumenta el valor de y.

Función decreciente

A medida que aumenta el valor de x, disminuye el valor de y.

Función constante

A medida que aumenta el valor de x, se mantiene el mismo valor en y.

EJEMPLOS DE GRÁFICAS DE FUNCIÓN LINEAL

En el ejercicio te indica que tienes que representar la siguiente función lineal:

• f(x)= x-1 

teniendo en cuenta el modelo de dicha función, marcamos el punto en 1 sobre el eje "x", y la el otro termino, sabemos que cuando no hay ningún número a la vista, se coloca el uno, y trabajamos con el nominador y denominador (fracción) , el 1 debajo tiene un 1, entonces subimos 1 lugar y corremos 1 lugar hacia la derecha porque es positivo, esto se realiza por encima del eje "y", y marcamos el lugar de encuentro, quedando finalmente la recta de esta manera:

• f(x)=-2x+2

FUNCIÓN CUADRÁTICA

• A la función de segundo grado f(x)= a.x²+b.x+c, siendo a, b, y c números reales y a ≠ 0, se denomina función cuadrática.

Y= a . x² + b . x + c

• La representación gráfica es una parábola : si a>0, las ramas hacia arriba  ⟶ cóncava hacia arriba; si a<0, las ramas hacia abajo ⟶ cóncava hacia abajo; si la a es positiva (+) las ramas van hacia arriba; si la a es negativa (-), las ramas van hacia abajo.

• Ejemplos

De un cuadrado de 4 cm de lado, se cortan en las esquinas triángulos rectángulos isósceles cuyos lados iguales miden x.

1. escribe el área del octógono que resulta en función de x.

Hace cinco años, la población de una pequeña comunidad indígena era de 500 personas. Como consecuencia de su integración con otras comunidades, la población ascencio a 4000 personas. Suponiendo que la población crece en forma lineal:

expresen mediante una fórmula la cantidad de habitantes en función del tiempo.

indiquen aproximadamente cuando llegara la población a 10000 habitantes.