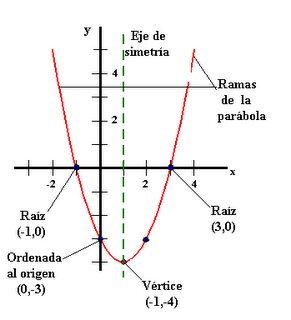
El
vértice de la parábola corresponde al máximo o mínimo de la función
La coordenada X (horizontal) del vértice
se obtiene con la siguiente ecuación:
La coordenada Y (vertical) del vértice
se obtiene sustituyendo la coordenada x calculada con la expresión anterior y
sustituyéndola en la función de la parábola correspondiente.
Eje de simetría
La recta vertical que parte la parábola en dos mitades simétricas y pasa por el vértice.
La recta vertical que parte la parábola en dos mitades simétricas y pasa por el vértice.
Por ejemplo, el vértice de la parabola y
= x2 – 2x -3 es
Vértice
y eje de simetría de la parábola
Raíces
Las raíces son los puntos donde la parábola corta el eje horizontal.
Las raíces son los puntos donde la parábola corta el eje horizontal.
Una parábola puede tener 2 raíces, una
raíz o ninguna. En otras palabras, la función puede cortar el eje “x” en dos
puntos, un punto o no cortarla como lo ilustra la figura:
Las
raíces de una parábola
Las raíces se obtienen igualando la
función a cero y resolviendo para “x”.
ax2 + bx + c =
0
En donde la solución general para
cualquier ecuación de segundo grado está dado por:
Por ejemplo, las raíces de la parabola y
= x2 – 2x -3 son:
a = 1; b = -2; c = -3
X1 = -1 ; X2 =
3
ECUACIÓN POLINÓMICA, CANÓNICA Y FACTORIZADA
PARA LA ECUACIÓN CANÓNICA:
cuadrado del binomio o propiedad distributiva
(x+3)2= (x+3) . (x+3)
x2+3x+3x+9
x2+6x+9
ECUACION CANONICA A POLINOMICA
Por ejemplo:
f(x) = a(x-h)^2 + k
primero desarrollarás el cuadrado del binomio
f(x) = a(x^2 - 2hx + h^2) + k
y luego efectúas el paréntesis
f(x) = ax^2 - 2ahx + ah^2 + k.
Por ejemplo:
f(x) = 2(x-3)^2 + 5
f(x) = 2(x^2 - 6x + 9) +5
f(x) = 2x^2 - 12x + 18 + 5
f(x) = 2x^2 - 12x + 23

No hay comentarios:
Publicar un comentario