PROBABILIDAD
martes, 29 de noviembre de 2016
TEMA N°6: "Funciones exponenciales"
FUNCIONES EXPONENCIALES
Ejemplos
| x | y = 2x |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
TEMA N°5: "Funciones racionales"
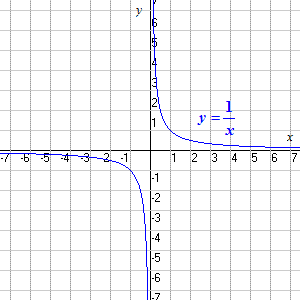
FUNCIONES RACIONALES
- Es una función que puede escribirse como cociente de dos polinomios.
- Si el denominador es un número (un polinomio de grado 0), entonces la función es un polinomio. Por lo tanto, las funciones polinómicas son funciones racionales.
- A medida que aumenta el factor que multiplica a x, la gráfica va aumentando hacia arriba. crecen hacia arriba respecto a la superficie.
TEMA N°4: "Función cuadrática"
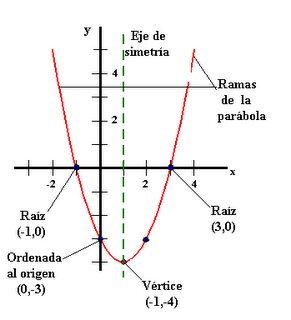
El
vértice de la parábola corresponde al máximo o mínimo de la función
La coordenada X (horizontal) del vértice
se obtiene con la siguiente ecuación:
La coordenada Y (vertical) del vértice
se obtiene sustituyendo la coordenada x calculada con la expresión anterior y
sustituyéndola en la función de la parábola correspondiente.
Eje de simetría
La recta vertical que parte la parábola en dos mitades simétricas y pasa por el vértice.
La recta vertical que parte la parábola en dos mitades simétricas y pasa por el vértice.
Por ejemplo, el vértice de la parabola y
= x2 – 2x -3 es
Vértice
y eje de simetría de la parábola
Raíces
Las raíces son los puntos donde la parábola corta el eje horizontal.
Las raíces son los puntos donde la parábola corta el eje horizontal.
Una parábola puede tener 2 raíces, una
raíz o ninguna. En otras palabras, la función puede cortar el eje “x” en dos
puntos, un punto o no cortarla como lo ilustra la figura:
Las
raíces de una parábola
Las raíces se obtienen igualando la
función a cero y resolviendo para “x”.
ax2 + bx + c =
0
En donde la solución general para
cualquier ecuación de segundo grado está dado por:
Por ejemplo, las raíces de la parabola y
= x2 – 2x -3 son:
a = 1; b = -2; c = -3
X1 = -1 ; X2 =
3
ECUACIÓN POLINÓMICA, CANÓNICA Y FACTORIZADA
PARA LA ECUACIÓN CANÓNICA:
cuadrado del binomio o propiedad distributiva
(x+3)2= (x+3) . (x+3)
x2+3x+3x+9
x2+6x+9
ECUACION CANONICA A POLINOMICA
Por ejemplo:
f(x) = a(x-h)^2 + k
primero desarrollarás el cuadrado del binomio
f(x) = a(x^2 - 2hx + h^2) + k
y luego efectúas el paréntesis
f(x) = ax^2 - 2ahx + ah^2 + k.
Por ejemplo:
f(x) = 2(x-3)^2 + 5
f(x) = 2(x^2 - 6x + 9) +5
f(x) = 2x^2 - 12x + 18 + 5
f(x) = 2x^2 - 12x + 23
TEMA N°3: "Funcion lineal"

- La grafica de una funcion lineal esta formada por puntos alineados.
- El coeficiente m es la pendiente y la representa cuanto varia f(x) por cada unidad que aumenta x.
- el coeficiente b es la ordenada al origen, o sea el punto en que la grafica corta al eje y.
Ejemplo: f(x)= 1 x +3
2
a= 1
2
b= 3
- El valor de la pendiente determina que una fuencion sea creciente, decreciente o constante.
- cero o raiz de la funcion es el corte de la grafica con el eje x.
- Para averiguar la raiz:
Raiz (igualar la funcion a 0)
1 x +3=0
2
1 x = -3
2
x= -3: 1
2
x= -6
- Para igualar la pendiente(si se conocen dos puntos) :
Dados dos puntos (x1,y1) ; (x2,y2)
a= y2-y1
x2-x1
- Ecuacion de la recta:
Dados los puntos (-2,4) y (1,5) hallar la ecuacion de la recta.
↓ ↘y1 ↓ ↘ y2
x1 x2
a= 5-4= 1
1-(-2) 3
y= a.x+b
5= 1.1+b
3
5=1+b
3
5-1=b
3
14=b
3
- Perpendicularidad y paralelismo
rectas paralelas: si sus pendientes son iguales.
rectas perpendiculares: si sus pendientes son opuestas e inversas.
TEMA N°1: "Clasificación numérica"
CONJUNTOS NUMÉRICOS

Los números naturales
Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:
N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
Los números enteros
Los números enteros son del tipo:
 = {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
= {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}Los números racionales
Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.

Los números irracionales
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es  , que se define como la relación entre la longitud de la circunferencia y su diámetro.
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
 , que se define como la relación entre la longitud de la circunferencia y su diámetro.
, que se define como la relación entre la longitud de la circunferencia y su diámetro. = 3.141592653589...
= 3.141592653589...Números reales
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por  .
.
 .
.TEMA N°2: Sucesiones.
Sucesiones: concepto, termino general, tipos.
- Sucesión
Una sucesión es un conjunto de números reales, cada número es denominado termino, cada sucesión tiene un primer termino y a cada termino le sigue otro termino.
- Termino general
Primero termino: a1
Ejemplo: hallar los 6 primeros términos y la suma de estos.
an
|
3.n+1
|
n/n+1
|
a1
|
4
|
1/2
|
a2
|
7
|
2/3
|
a3
|
10
|
3/4
|
a4
|
13
|
4/5
|
a5
|
16
|
5/6
|
a6
|
19
|
6/7
|
suma
|
69
|
- Tipos de sucesiones numéricas: aritméticas y geométricas.
Aritméticas: son simples, la diferencia entre un término "x" y el siguiente siempre va a ser constante, esto quiere decir que a medida que van siguiendo los términos se van sumando o restando una constante que se la llama RAZÓN.
El término general se haya con la siguiente formula:
AN: A1+R.(N-1)
r: razón
a1: 1° término
n: n° término
Para calcular la suma de los primeros "n" términos se utiliza la formula:
Sn: (a1+an).n
2
Por ejemplo: hallar el término general de las siguientes sucesiones.
3,6,9,12
Lo podemos resolver con la fórmula antes nombrada de término general an=a1+r (n-1)
an= 3+3. (n-1)=3+3n-3=3n
Geométricas: es cuando cada término se obtiene a partir del anterior multiplicando siempre por un mismo número. La razón entre cada término y el anterior es constante.
Para calcular la razón : razón←q= an+1
an
n-1
El término general puede expresarse como: an=a1.q
n
Para sumar los primeros n términos: sn=a1.(q -1)
Ejemplo: 2,4,8,16,32
Suscribirse a:
Comentarios (Atom)




